5  Exploratory Factor Analysis

5.1 The Common Factor Model

In the common factor model, variances can be partitioned into common variances and unique variances. Common variances are those due to the common factor, while unique variances include all sources of variance not attributable to the common factor. Unique variance can be decomposed into specific and error variances. Specific variance is due to systematic sources of variability that are unique to the observed indicator. Error variance is due to random measurement variance.

\[ x = \tau + \varepsilon \tag{5.1}\]

\[ \sigma^2_x = \sigma^2_T + \sigma^2_{\varepsilon} \tag{5.2}\]

which we can directly compare to the common factor model we will learn about in this chapter:

\[ x = \mu + \Lambda f + \varepsilon \tag{5.3}\]

\[ Var(x) = \Lambda \Phi \Lambda^T + \psi = \Sigma(\theta) \tag{5.4}\]

5.1.1 Think about these situations

What do you do when you have a large number of variables you are considering as predictors of a dependent variable?

  • Often, subsets of these variables are measuring the same, or very similar things.
  • We might like to reduce the variables to a smaller number of predictors.

What if you are developing a measurement scale and have a large number of items you think measure the same construct

  • You might want to see how strongly the items are related to the construct.

To make sense of these abstract goals, and to help explain the procedures of EFA in this chapter, I will use an example from chapter 4 of Desjardins and Bulut (2018).

This example uses as subset of the interest data which fictitious survey data on cognitive, personality and interest items. A subset of items related to cognition will be used here to follow the description in that text.

First, load the hemp package and create a data frame called cognition.

library(hemp)
cognition <- subset(interest, select = vocab:analyrea)

Then look at a summary of the data.

summary(cognition)
     vocab             reading           sentcomp           mathmtcs      
 Min.   :-2.62000   Min.   :-2.4700   Min.   :-2.47000   Min.   :-3.7100  
 1st Qu.:-0.60500   1st Qu.:-0.5175   1st Qu.:-0.55000   1st Qu.:-0.4925  
 Median : 0.04000   Median : 0.1850   Median : 0.10500   Median : 0.1000  
 Mean   : 0.09016   Mean   : 0.1350   Mean   : 0.07356   Mean   : 0.1055  
 3rd Qu.: 0.86000   3rd Qu.: 0.7975   3rd Qu.: 0.77500   3rd Qu.: 0.9200  
 Max.   : 2.63000   Max.   : 2.7000   Max.   : 2.73000   Max.   : 3.0600  
    geometry          analyrea      
 Min.   :-3.3200   Min.   :-2.8300  
 1st Qu.:-0.5600   1st Qu.:-0.4825  
 Median : 0.0900   Median : 0.2000  
 Mean   : 0.1125   Mean   : 0.1750  
 3rd Qu.: 0.7675   3rd Qu.: 0.8375  
 Max.   : 3.8600   Max.   : 3.5000

Looking at the output, we see that the means of these variables are close to zero, with the spread of the data being roughly symmetrical around the mean, suggesting that these variables may have been standardized, which entails transforming them into z-scores. If this is the case, we would expect the variances (and standard deviations) to be about 1. We can look at the variances of each of the variables with the combination of the apply() and var() functions. The apply() function allows us to repeat another function over either the rows or columns of a two dimensional data object, such as a data frame. The MARGIN = 2, argument tells the function to appply var() over the columns (MARGIN = 1 would use rows). And the FUN = var argument identifies the function to apply over columns. Note the absence of parentheses after the function var in the call.

apply(cognition, MARGIN = 2, FUN = var)
    vocab   reading  sentcomp  mathmtcs  geometry  analyrea 
0.9966514 0.9811568 0.9834142 1.1117325 1.0686631 1.1170926

This supports our suspicion of standardized variables. It is often good to have items on the same or similar scales for factor analysis.

The cognition data are organized so that each individual is represented by one row, and their score on each item is contained in a separate column. This format is often called the wide format. To conduct factor analysis (and many other types of analysis) the long format is needed. Instead of separate columns containing the scores for each item, the long format would have all scores in one column and a categorical variable that captures which item each score represents. Therefore, each individual would be represented by multiple rows, one for each item, hence the long in long format.

Below, the reshape() function from base R is used to reshape the data from wide to long format, and store this new data frame in an object named cognition_l (note that the lowercase letter L is appended to the name, not the number 1). This function takes the cognition data (data = cognition), indicated that the first through the sixth columns are the ones to convert (varying = 1:6), names the variable that will contain the cell values from the original data as “score” (v.names = "score"), names the new character variable that describes which column the scores came from as “indicator” (timevar = "indicator"), uses the column names of those columns as the what will become the labels in the new categorical variable, which is a factor in R (times = names(cognition)), and finally tells the function to tranform the data into the “long” format (direction = "long"). The new To learn more about this function you can type ?reshape in to the R console. This transformation create the indicator variable as a charater variable, so we also convert it into a factor.

cognition_l <- reshape(data = cognition,
                       varying = 1:6,
                       v.names = "score",
                       timevar = "indicator",
                       times = names(cognition),
                       direction = "long")

# Convert "indicator" into factor using the values as labels
cognition_l$indicator <- factor(cognition_l$indicator)

Looking at the first few rows, we can see that this data indeed has one column for the numeric values in the cells of the original data, and a factor variable containing the indicator type.

head(cognition_l[order(cognition_l$id), ])
           indicator score id
1.vocab        vocab  1.67  1
1.reading    reading  1.67  1
1.sentcomp  sentcomp  1.46  1
1.mathmtcs  mathmtcs  0.90  1
1.geometry  geometry  0.49  1
1.analyrea  analyrea  1.65  1

With this long data frame, we can look at the univariate distribution of the 6 indicators. Below I show how to do that with the lattice package and the ggplot2 package.

library(lattice)
histogram(~ score | indicator, data = cognition_l)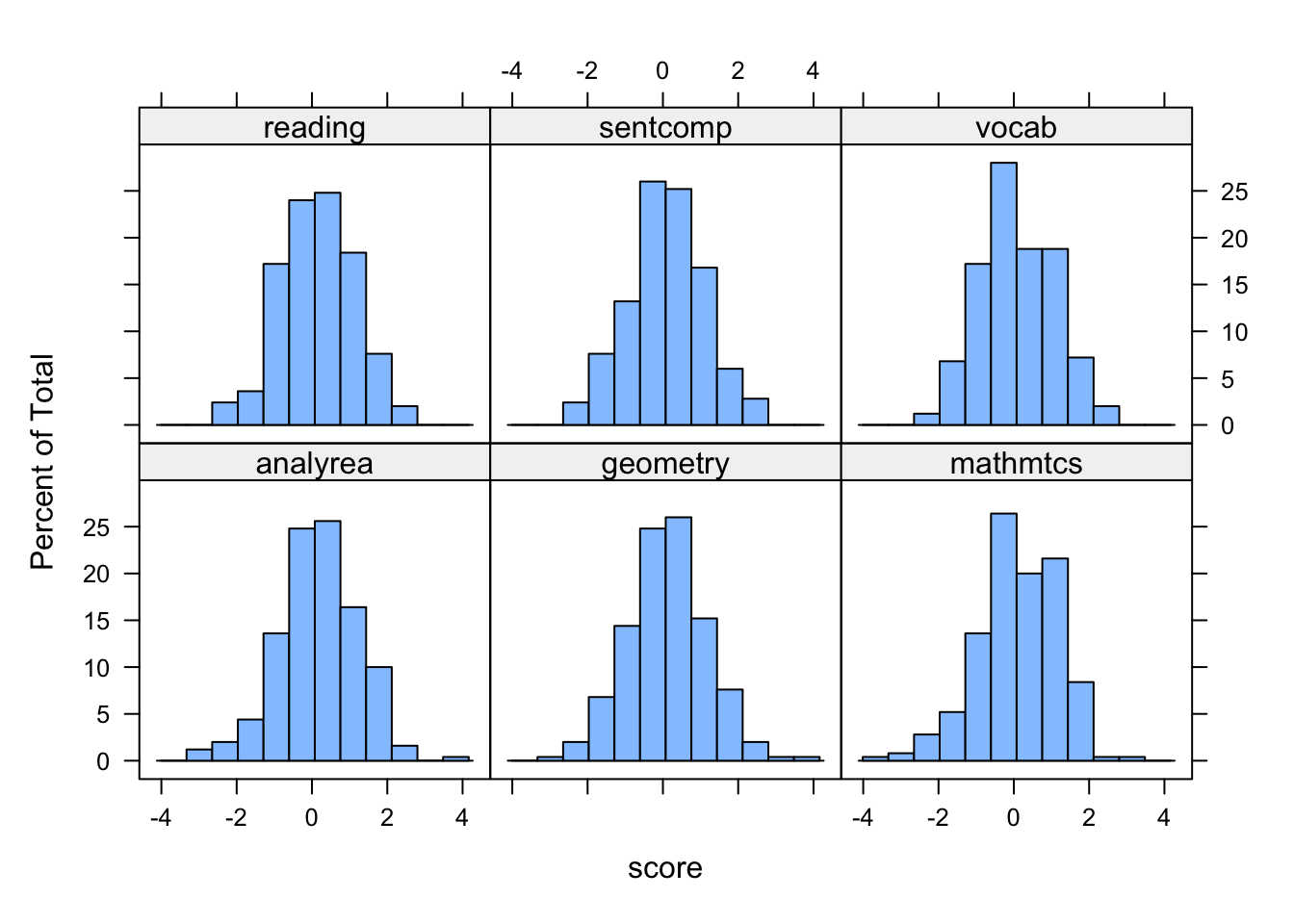

library(ggplot2)
ggplot(cognition_l, aes(x = score)) + geom_histogram() +
  facet_wrap(~ indicator )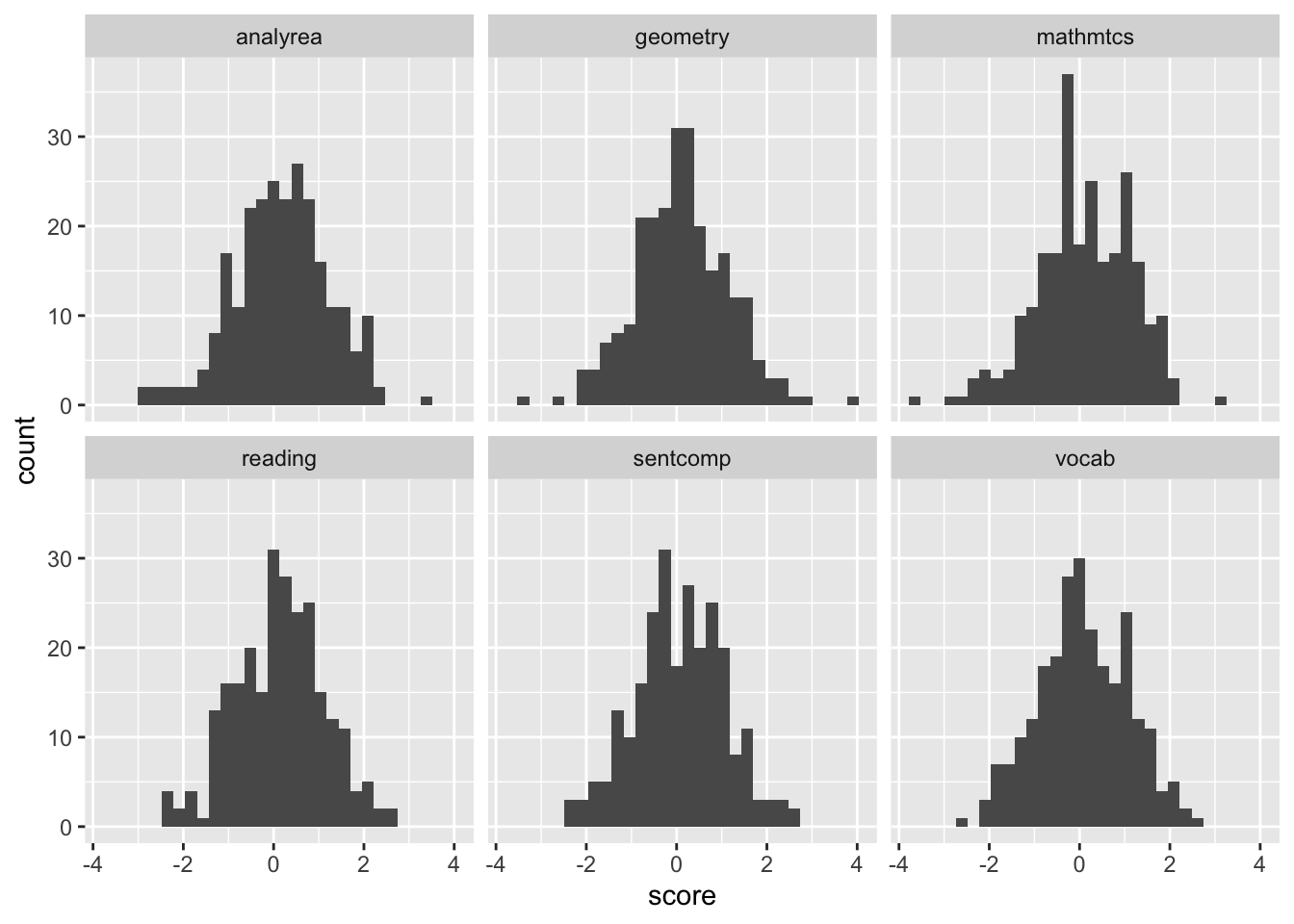

From these plots it seems reasonable to assume these variables are normally distributed, and we also see that these indicators have similar variances and are centered around zero, consistent with them being standardized.

Next we can explore bivariate relations between the indicators. Before calculating correlation coefficients, it is helpful to plot the bivariate relations to evalute the assumptions of correlation coefficients as well as for the factor analysis. The pairs() function is useful for this.

pairs(cognition)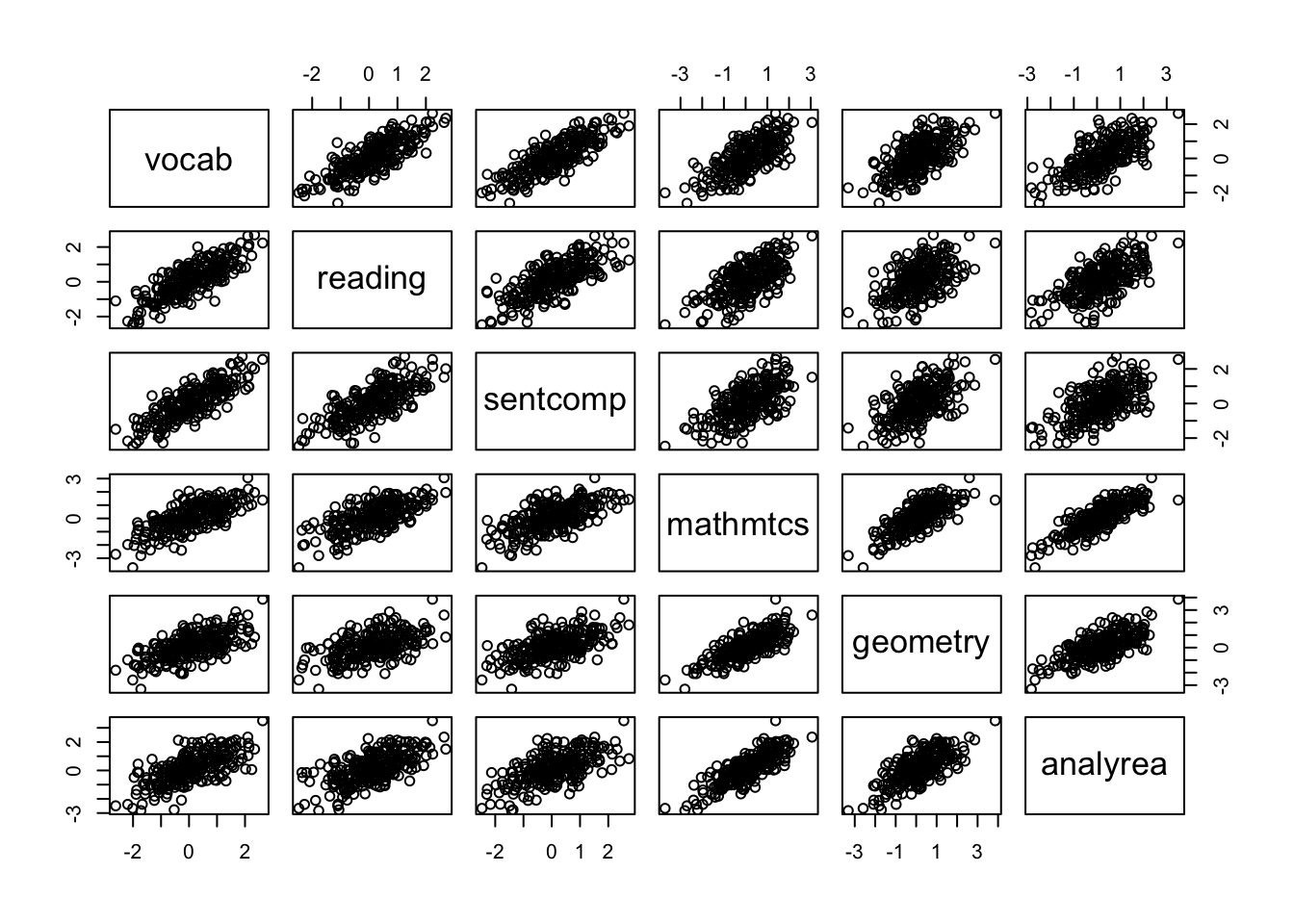

5.1.2 Correlation Coefficient

Pearson product-moment correlation:

\[ r_{xy} = \frac{\Sigma_{n=1}^n (x_k - \bar{x})(y_i - \bar{y})}{\sqrt{\Sigma_{n=1}^n(x_i - \bar{x})^2} \sqrt{\Sigma_{n=1}^n(y_i - \bar{y})^2}} = \frac{s_{xy}}{s_x s_y}. \]

The equation looks very daunting, until you see that it is just the covariance of \(x\) and \(y\) divided by the product of their standard deviations.

correlations <- cor(cognition)
round(correlations, 3)
         vocab reading sentcomp mathmtcs geometry analyrea
vocab    1.000   0.803    0.813    0.708    0.633    0.673
reading  0.803   1.000    0.725    0.660    0.526    0.636
sentcomp 0.813   0.725    1.000    0.618    0.575    0.618
mathmtcs 0.708   0.660    0.618    1.000    0.774    0.817
geometry 0.633   0.526    0.575    0.774    1.000    0.715
analyrea 0.673   0.636    0.618    0.817    0.715    1.000
cor_diff <- correlations - cor(cognition[-c(202, 53, 111), ])
round(cor_diff, 3)
         vocab reading sentcomp mathmtcs geometry analyrea
vocab    0.000   0.005    0.009    0.000    0.021    0.009
reading  0.005   0.000    0.010    0.016    0.025    0.021
sentcomp 0.009   0.010    0.000    0.009    0.027    0.014
mathmtcs 0.000   0.016    0.009    0.000   -0.004    0.005
geometry 0.021   0.025    0.027   -0.004    0.000    0.015
analyrea 0.009   0.021    0.014    0.005    0.015    0.000
bollen_plot(cognition, crit.value = 0.06)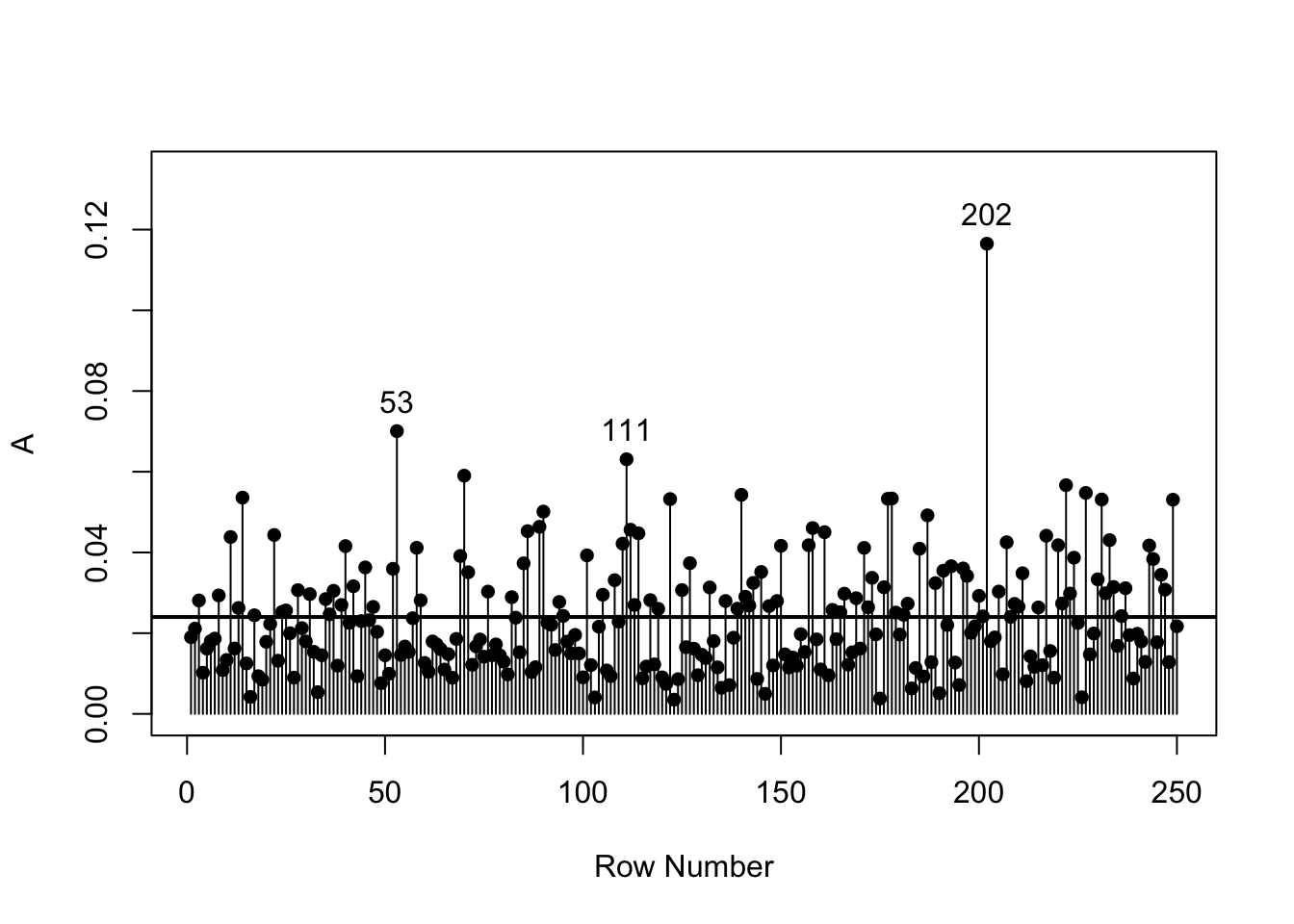

cognition[c(202, 53, 111), ]
    vocab reading sentcomp mathmtcs geometry analyrea
202  2.63    2.23     2.55     1.38     3.86     3.50
53  -0.38    0.99    -0.50     1.79    -0.19     2.13
111 -2.01   -2.47    -2.47    -3.71    -2.59    -2.67
apply(cognition, 2, min)
   vocab  reading sentcomp mathmtcs geometry analyrea 
   -2.62    -2.47    -2.47    -3.71    -3.32    -2.83 
apply(cognition, 2, max)
   vocab  reading sentcomp mathmtcs geometry analyrea 
    2.63     2.70     2.73     3.06     3.86     3.50

5.2 Solutions

  1. Principal Components Analysis

    • transforming the original variables into a new set of linear combinations (pricipal components).

  2. Factor Analysis

    • setting up a mathematical model to estimate the number or factors

5.2.1 Principal Components Analysis

  • Concerned with explaining variance-covariance structure of a set of variables.
  • PCA attempts to explain as much of the total variance among the observed variables as possible with a smaller number of components.
  • Because the variables are standardized prior to analysis, the total amount of variance available is the number of variables.
  • The goal is data reduction for subsequent analysis.
  • Variables cause components.
  • Components are not representative of any underlying theory.

5.2.2 Factor Analysis

  • The goal is understanding underlying constructs.
  • Uses a modified correlation matrix (reduced matrix)
  • factors cause the variables.
  • Factors represent theoretical constructs.
  • Focuses on the common variance of the variables, and purges the unique variance.

5.2.3 Steps in Factor Analysis

  1. Choose extraction method
    • So far we’ve focused on PCA
    • EFA is often preferred if you are developing theory
  2. Determine the number of components/factors
    • Kaiser method: eigenvalues > 1
    • Scree plot: All components before leveling off
    • Horn’s parallel analysis: components/factors greater than simulated values from random numbers
  3. Rotate Factors
    • Orthogonal
    • Oblique
  4. Interpret Components/Factors

5.2.4 “Little Jiffy” method of factor analysis

  1. Extraction method : PCA
  2. Number of factors: eigenvalues > 1
  3. Rotation: orthogonal(varimax)
  4. Interpretation

Following these steps without thought can lead to many problems (see Preacher and MacCallum 2003)

5.2.5 Eigenvalues

Eigenvalues represent the variance in the variables explained by the success components.

5.2.6 Determining the Number of Factors

  1. Kaiser criterion: Retain only factors with eigenvalues > 1. (generally accurate)
  2. Scree plot: plot eigenvalues and drop factors after leveling off.
  3. Parallel analysis: compare observed eigenvalues to parallel set of data from randomly generated data. Retain factors in original if eigenvalue is greater than random eigenvalue.
  4. Factor meaningfulness is also very important to consider.

5.2.6.1 Kaiser

Retain factors with eigenvalues greater than 1

eigen_decomp <- eigen(correlations)
round(eigen_decomp$values, 3)
[1] 4.436 0.676 0.322 0.245 0.168 0.152

5.2.6.2 Scree Plot

scree(cognition, pc = FALSE)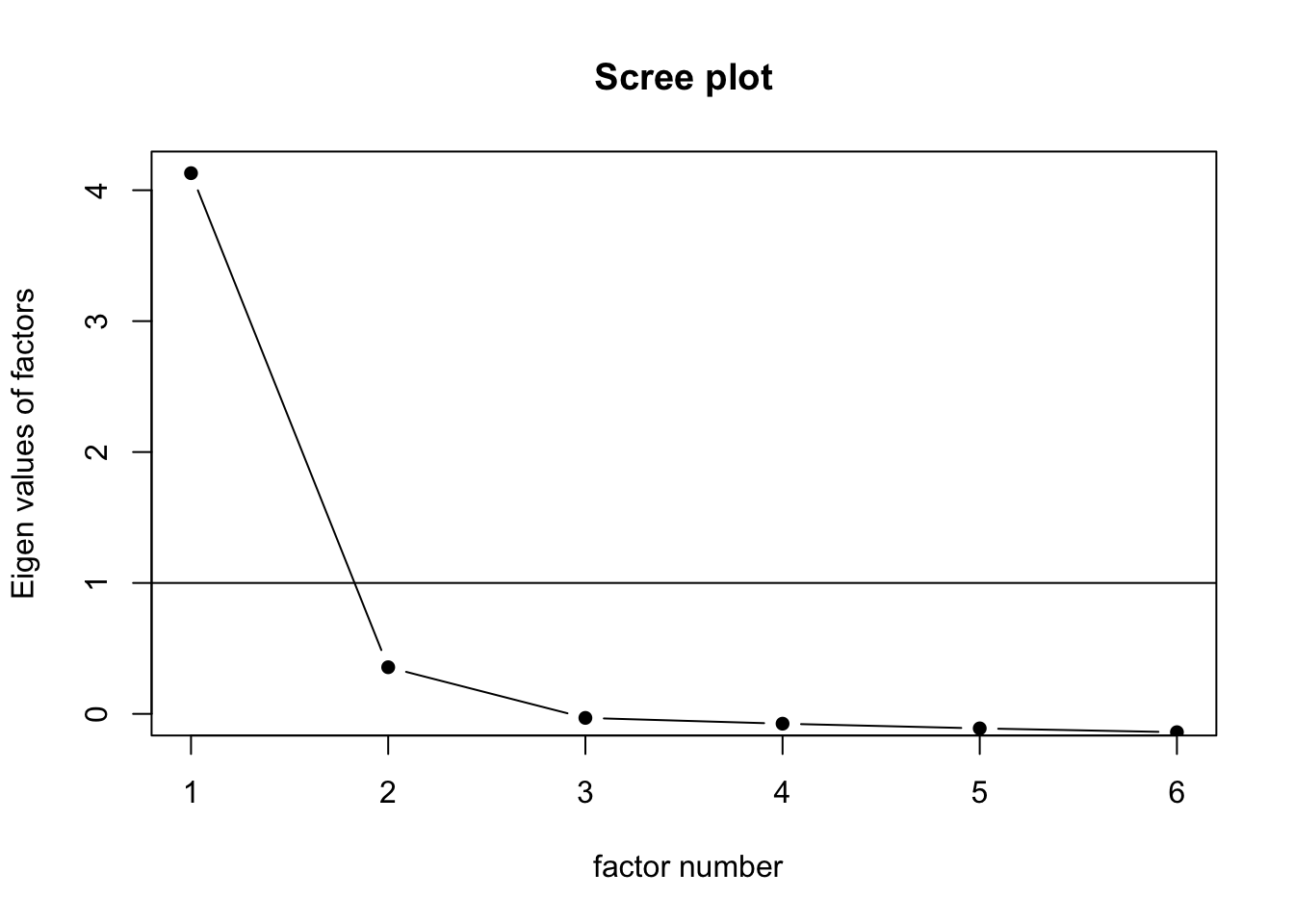

5.2.6.3 Horn’s Parallel Analysis

fa.parallel(cognition, fm = "ml")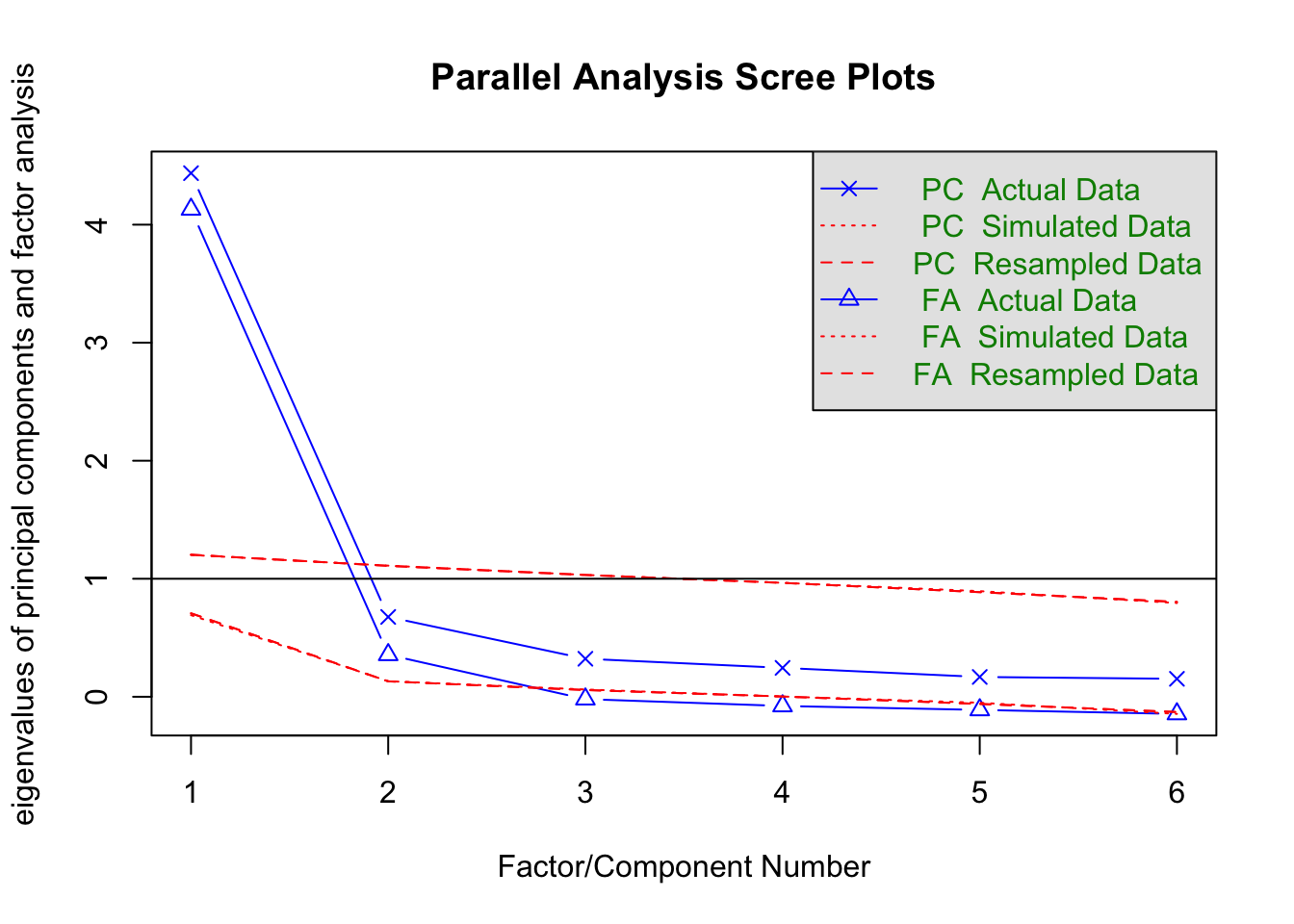

Parallel analysis suggests that the number of factors =  2  and the number of components =  1

Using these conventions we can rewrite the classic test score model as:

principal(correlations)
Principal Components Analysis
Call: principal(r = correlations)
Standardized loadings (pattern matrix) based upon correlation matrix
          PC1   h2   u2 com
vocab    0.90 0.81 0.19   1
reading  0.84 0.71 0.29   1
sentcomp 0.84 0.71 0.29   1
mathmtcs 0.89 0.79 0.21   1
geometry 0.82 0.67 0.33   1
analyrea 0.86 0.75 0.25   1

                PC1
SS loadings    4.44
Proportion Var 0.74

Mean item complexity =  1
Test of the hypothesis that 1 component is sufficient.

The root mean square of the residuals (RMSR) is  0.09 

Fit based upon off diagonal values = 0.98
one_factor <- fa(r = cognition, nfactors = 1, rotate = "oblimin")
one_factor
Factor Analysis using method =  minres
Call: fa(r = cognition, nfactors = 1, rotate = "oblimin")
Standardized loadings (pattern matrix) based upon correlation matrix
          MR1   h2   u2 com
vocab    0.89 0.79 0.21   1
reading  0.81 0.65 0.35   1
sentcomp 0.80 0.65 0.35   1
mathmtcs 0.87 0.76 0.24   1
geometry 0.77 0.59 0.41   1
analyrea 0.84 0.70 0.30   1

                MR1
SS loadings    4.13
Proportion Var 0.69

Mean item complexity =  1
Test of the hypothesis that 1 factor is sufficient.

df null model =  15  with the objective function =  5.11 with Chi Square =  1257.24
df of  the model are 9  and the objective function was  0.71 

The root mean square of the residuals (RMSR) is  0.07 
The df corrected root mean square of the residuals is  0.1 

The harmonic n.obs is  250 with the empirical chi square  41.32  with prob <  4.4e-06 
The total n.obs was  250  with Likelihood Chi Square =  173.3  with prob <  1.3e-32 

Tucker Lewis Index of factoring reliability =  0.779
RMSEA index =  0.27  and the 90 % confidence intervals are  0.236 0.307
BIC =  123.61
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   MR1
Correlation of (regression) scores with factors   0.97
Multiple R square of scores with factors          0.94
Minimum correlation of possible factor scores     0.87
two_factor <- fa(r = cognition, nfactors = 2, rotate = "oblimin")
two_factor
Factor Analysis using method =  minres
Call: fa(r = cognition, nfactors = 2, rotate = "oblimin")
Standardized loadings (pattern matrix) based upon correlation matrix
           MR1   MR2   h2   u2 com
vocab     0.95  0.00 0.90 0.10   1
reading   0.83  0.02 0.72 0.28   1
sentcomp  0.87 -0.02 0.74 0.26   1
mathmtcs -0.03  0.96 0.89 0.11   1
geometry -0.02  0.84 0.68 0.32   1
analyrea  0.07  0.81 0.76 0.24   1

                       MR1  MR2
SS loadings           2.36 2.31
Proportion Var        0.39 0.38
Cumulative Var        0.39 0.78
Proportion Explained  0.51 0.49
Cumulative Proportion 0.51 1.00

 With factor correlations of 
    MR1 MR2
MR1 1.0 0.8
MR2 0.8 1.0

Mean item complexity =  1
Test of the hypothesis that 2 factors are sufficient.

df null model =  15  with the objective function =  5.11 with Chi Square =  1257.24
df of  the model are 4  and the objective function was  0.05 

The root mean square of the residuals (RMSR) is  0.01 
The df corrected root mean square of the residuals is  0.03 

The harmonic n.obs is  250 with the empirical chi square  1.42  with prob <  0.84 
The total n.obs was  250  with Likelihood Chi Square =  11.64  with prob <  0.02 

Tucker Lewis Index of factoring reliability =  0.977
RMSEA index =  0.087  and the 90 % confidence intervals are  0.031 0.148
BIC =  -10.44
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   MR1  MR2
Correlation of (regression) scores with factors   0.97 0.97
Multiple R square of scores with factors          0.94 0.94
Minimum correlation of possible factor scores     0.88 0.87

5.2.7 EFA with Categorical Data

SAPA_subset <- subset(SAPA, select = c(letter.7:letter.58,
                                       rotate.3:rotate.8))

fa.parallel(SAPA_subset, cor = "poly")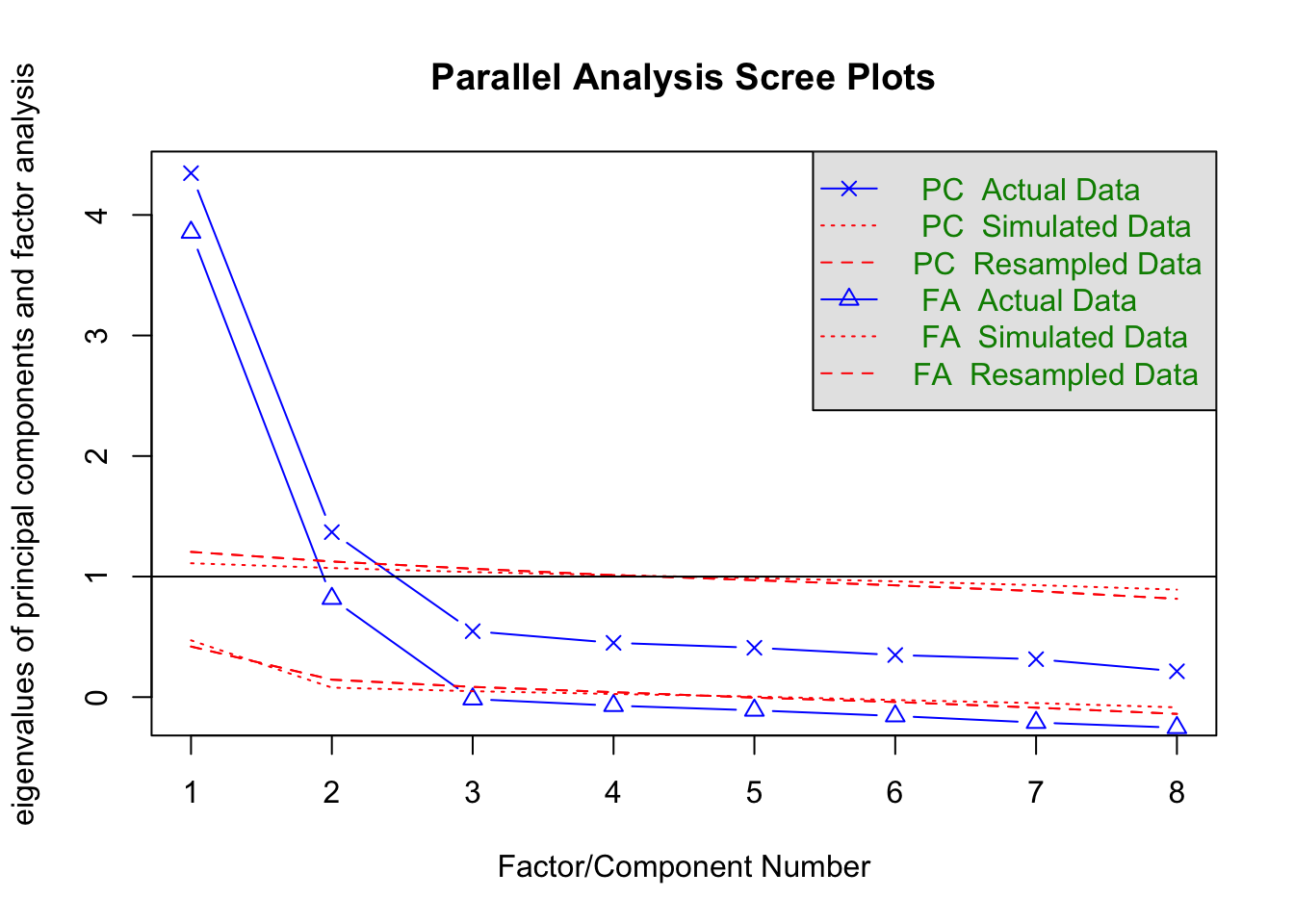

Parallel analysis suggests that the number of factors =  2  and the number of components =  2 
EFA_SAPA <- fa(r = SAPA_subset, nfactors = 2, rotate = "oblimin",
               cor = "poly")
EFA_SAPA
Factor Analysis using method =  minres
Call: fa(r = SAPA_subset, nfactors = 2, rotate = "oblimin", cor = "poly")
Standardized loadings (pattern matrix) based upon correlation matrix
            MR1   MR2   h2   u2 com
letter.7  -0.02  0.79 0.60 0.40 1.0
letter.33  0.01  0.70 0.50 0.50 1.0
letter.34 -0.02  0.80 0.63 0.37 1.0
letter.58  0.21  0.54 0.46 0.54 1.3
rotate.3   0.86 -0.02 0.72 0.28 1.0
rotate.4   0.82  0.10 0.77 0.23 1.0
rotate.6   0.77  0.05 0.64 0.36 1.0
rotate.8   0.86 -0.09 0.65 0.35 1.0

                       MR1  MR2
SS loadings           2.84 2.13
Proportion Var        0.36 0.27
Cumulative Var        0.36 0.62
Proportion Explained  0.57 0.43
Cumulative Proportion 0.57 1.00

 With factor correlations of 
     MR1  MR2
MR1 1.00 0.56
MR2 0.56 1.00

Mean item complexity =  1
Test of the hypothesis that 2 factors are sufficient.

df null model =  28  with the objective function =  4.26 with Chi Square =  6477.4
df of  the model are 13  and the objective function was  0.06 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.02 

The harmonic n.obs is  1523 with the empirical chi square  22.69  with prob <  0.046 
The total n.obs was  1525  with Likelihood Chi Square =  97.39  with prob <  5.3e-15 

Tucker Lewis Index of factoring reliability =  0.972
RMSEA index =  0.065  and the 90 % confidence intervals are  0.053 0.078
BIC =  2.1
Fit based upon off diagonal values = 1
Measures of factor score adequacy             
                                                   MR1  MR2
Correlation of (regression) scores with factors   0.95 0.92
Multiple R square of scores with factors          0.91 0.84
Minimum correlation of possible factor scores     0.81 0.68

5.3 Another Example

library("MPsychoR")
data("YouthDep")
item1 <- YouthDep[, 1]
levels(item1) <- c("0", "1", "1")
item2 <- YouthDep[, 14]
levels(item2) <- c("0", "1", "1")
table(item1, item2)
     item2
item1    0    1
    0 1353  656
    1  115  166
## ------ correlation coefficients
library("psych")
tetcor <- tetrachoric(cbind(item1, item2))
tetcor
Call: tetrachoric(x = cbind(item1, item2))
tetrachoric correlation 
      item1 item2
item1 1.00       
item2 0.35  1.00 

 with tau of 
item1 item2 
 1.16  0.36 
item1 <- YouthDep[, 1]
item2 <- YouthDep[, 14]
polcor <- polychoric(cbind(item1, item2))
polcor
Call: polychoric(x = cbind(item1, item2))
Polychoric correlations 
      item1 item2
item1 1.00       
item2 0.33  1.00 

 with tau of 
         1   2
item1 1.16 2.3
item2 0.36 1.2
draw.tetra(r = .35, t1 = 1.16, t2 = .36)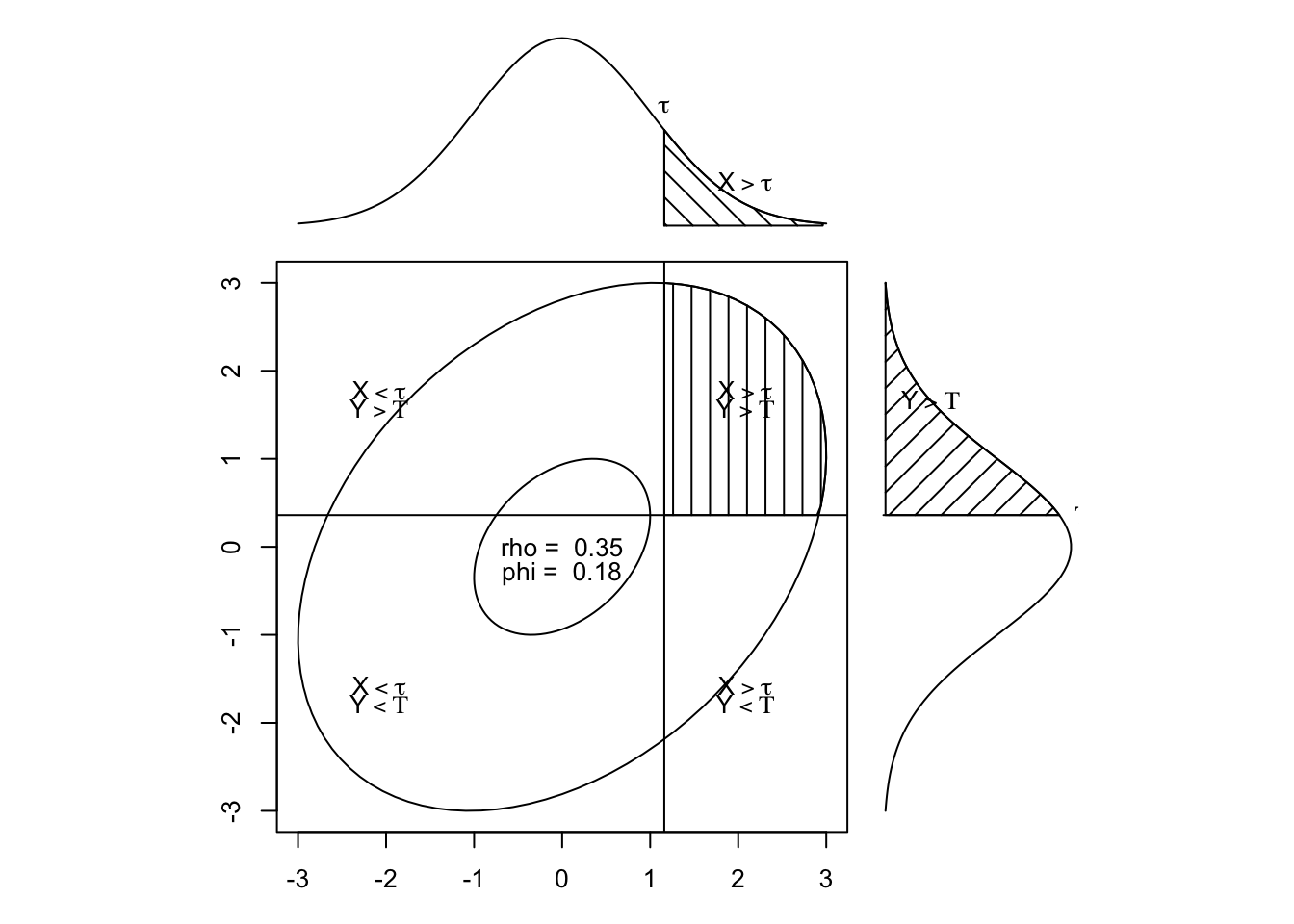

DepItems <- YouthDep[,1:26] 
Depnum <- data.matrix(DepItems) - 1  ## convert to numeric   
Rdep <- polychoric(Depnum)

5.3.1 Example data

lower <- "
1.00
0.70 1.00
0.65 0.66 1.00
0.62 0.63 0.60 1.00
"
cormat <- getCov(lower, names = c("d1", "d2", "d3", "d4"))

cormat
     d1   d2   d3   d4
d1 1.00 0.70 0.65 0.62
d2 0.70 1.00 0.66 0.63
d3 0.65 0.66 1.00 0.60
d4 0.62 0.63 0.60 1.00

5.3.2 Kaiser

Retain factors with eigenvalues greater than 1

eigen(cormat)$values
[1] 2.9311792 0.4103921 0.3592372 0.2991916

5.3.3 Scree Plot

scree(cormat, factors = FALSE)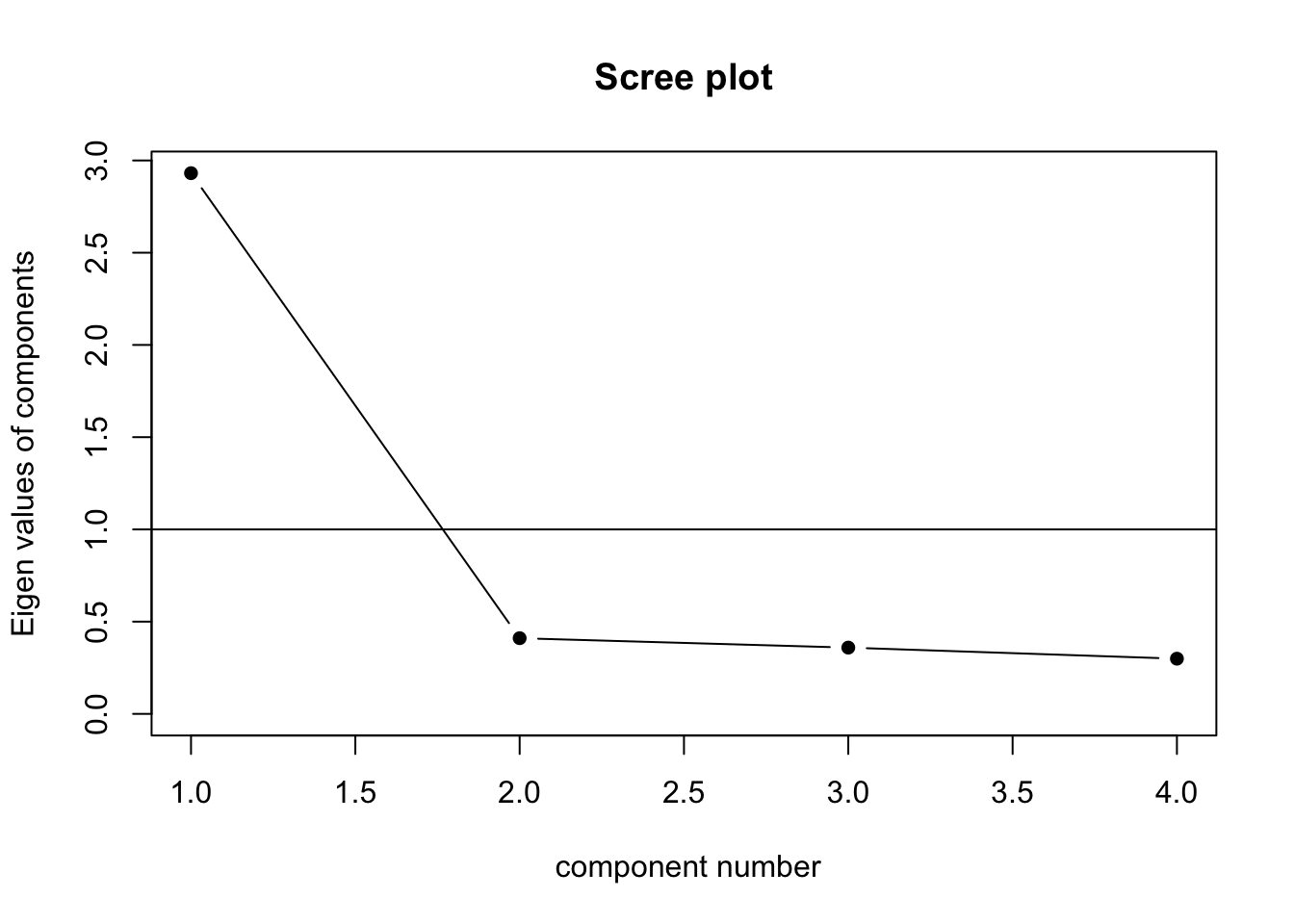

5.3.4 Horn’s Parallel Analysis

fa.parallel(cormat, fa = "pc")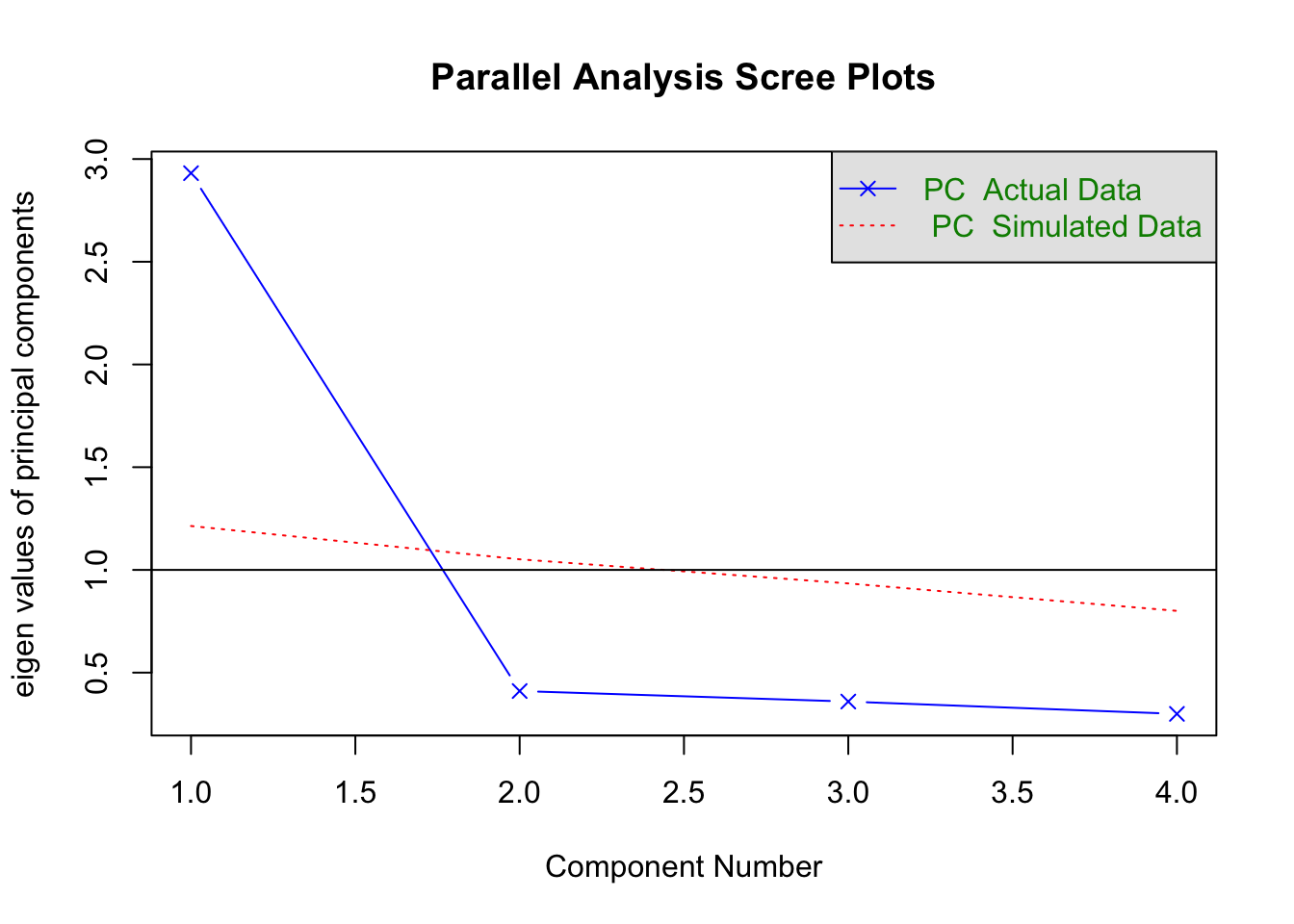

Parallel analysis suggests that the number of factors =  NA  and the number of components =  1

5.4 Another example

fa.parallel(Harman74.cor$cov, fa = "pc")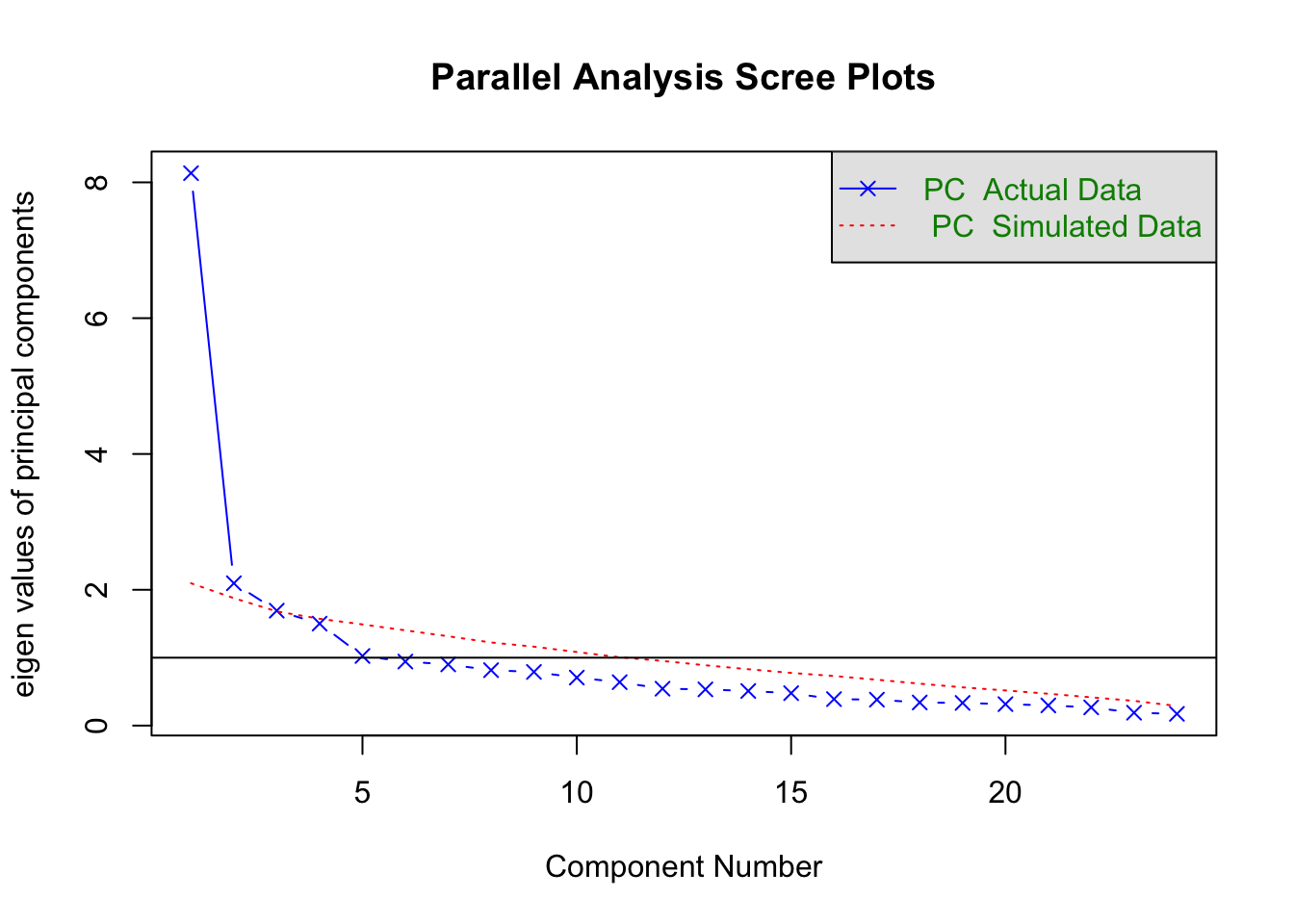

Parallel analysis suggests that the number of factors =  NA  and the number of components =  2

5.4.1 Rotation

  • Principal components are derived to maximize the variance accounted for (data reduction).
  • Rotation is done to make the factors more interpretable (i.e. meaningful).
  • Two major classes of rotation:
    • Orthogonal - new factors are still uncorrelated, as were the initial factors.
    • Oblique - new factors are allowed to be correlated.

Essentially reallocates the loadings. The first factor may not be the one accounting for the most variance.

5.4.2 Orthogonal Rotation

  1. Quartimax - idea is to clean up the variables. Rotation done so each variable loads mainly on one factor. Problematic if there is a general factor on which most or all variables load on (think IQ).

  2. Varimax - to clean up factors. So each factor has high correlation with a smaller number of variables, low correlation with the other variables. Generally makes interpretation easier.

5.4.3 Oblique Rotation

  • Often correlated factors are more reasonable.
  • Therefore, oblique rotation is often preferred.
  • But interpretation is more complicated.

5.4.4 Factor Matrices

  1. Factor pattern matrix:
    • includes pattern coefficients analogous to standardized partial regression coefficients.
    • Indicated the unique importance of a factor to a variable, holding other factors constant.
  2. Factor structure matrix:
    • includes structure coefficients which are simple correlations of the variables with the factors.

5.4.5 Which matrix should we interpret?

  • When orthogonal rotation is used interpret structural coefficients (but they are the same as pattern coefficients).

  • When oblique rotation is used pattern coefficients are preferred because they account for the correlation between the factors and they are parameters of the correlated factor model (which we will discuss next class).

5.4.6 Which variables should be used to interpret each factor?

  • The idea is to use only those variables that have a strong association with the factor.
  • Typical thresholds are |.30| or |.40|.
  • Content knowledge is critical.

5.5 Tom Swift’s Electric Factor Analysis Factory

5.5.1 Steps in Factor Analysis

  1. Choose extraction method
    • So far we’ve focused on PCA
  2. Determine the number of components/factors
    • Kaiser method: eigenvalues > 1
    • Scree plot: All components before leveling off
    • Horn’s parallel analysis: components/factors greater than simulated values from random numbers
  3. Rotate Factors
    • Orthogonal
    • Oblique
  4. Interpret Components/Factors

5.5.2 “Little Jiffy” method of factor analysis

  1. Extraction method : PCA
  2. Number of factors: eigenvalues > 1
  3. Rotation: orthogonal(varimax)
  4. Interpretation

5.5.3 Metal Boxes

Functional Definitions of Tom Swift’s Original 11 Variables
Dimension Derivation
Thickness x
Width y
Length z
Volume xyz
Density d
Weight xyzd
Surface area 2(xy + xz + yz)
Cross-section yz
Edge length 4(x + y + z)
Diagonal length (x^2)
Cost/lb c 
'data.frame':   63 obs. of  11 variables:
 $ thick   : num  1.362 1.83 0.567 1.962 1.762 ...
 $ width   : num  1.71 4.01 1.86 1.71 1.95 ...
 $ length  : num  4.93 5.2 4.31 3.91 4.1 ...
 $ volume  : num  10.02 39.59 8.02 16.02 15.92 ...
 $ density : int  17 6 4 14 7 4 1 1 14 8 ...
 $ weight  : num  170 240.1 32.1 224 111.6 ...
 $ surface : num  34 76.1 28.1 39.5 40.4 ...
 $ crosssec: num  9.87 19.94 7.94 8.22 8.24 ...
 $ edge    : num  31.9 43.9 27.9 31.5 31.7 ...
 $ diagonal: num  900 2025 441 576 576 ...
 $ cost    : num  9.73 14.13 -2.92 6.78 7.62 ...

5.5.4 Correlations

Correlations between dimensions
thick width length volume density weight surface crosssec edge diagonal cost
thick 1.00 0.43 0.28 0.78 -0.16 0.53 0.69 0.40 0.60 0.48 -0.01
width 0.43 1.00 0.50 0.78 -0.10 0.54 0.86 0.88 0.84 0.74 0.04
length 0.28 0.50 1.00 0.60 0.13 0.54 0.73 0.82 0.82 0.87 0.22
volume 0.78 0.78 0.60 1.00 -0.09 0.69 0.97 0.81 0.90 0.86 0.07
density -0.16 -0.10 0.13 -0.09 1.00 0.53 -0.05 0.01 -0.02 0.04 0.83
weight 0.53 0.54 0.54 0.69 0.53 1.00 0.71 0.64 0.69 0.68 0.55
surface 0.69 0.86 0.73 0.97 -0.05 0.71 1.00 0.93 0.97 0.92 0.11
crosssec 0.40 0.88 0.82 0.81 0.01 0.64 0.93 1.00 0.95 0.94 0.15
edge 0.60 0.84 0.82 0.90 -0.02 0.69 0.97 0.95 1.00 0.92 0.14
diagonal 0.48 0.74 0.87 0.86 0.04 0.68 0.92 0.94 0.92 1.00 0.17
cost -0.01 0.04 0.22 0.07 0.83 0.55 0.11 0.15 0.14 0.17 1.00

5.5.5 Eigenvalues > 1

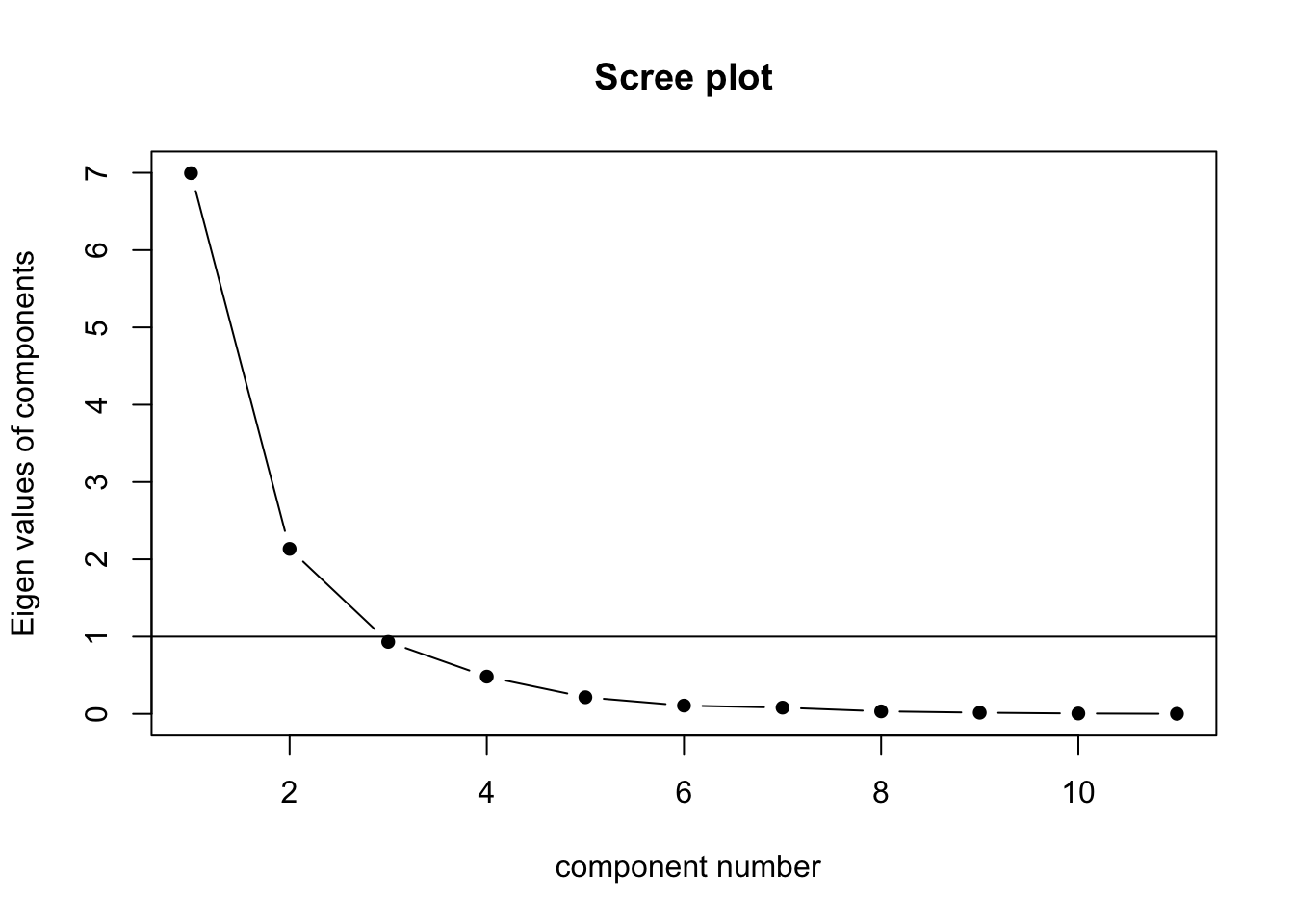
5.5.6 Orthogonal Rotation


Loadings:
         RC1    RC4    RC3    RC2    RC5   
thick                   0.962              
width            0.926                     
length    0.955                            
volume                                     
density                        0.942       
weight                                     
surface                                    
crosssec         0.705                     
edge                                       
diagonal  0.775                            
cost                           0.960       

                 RC1   RC4   RC3   RC2   RC5
SS loadings    3.165 2.913 2.226 2.193 0.263
Proportion Var 0.288 0.265 0.202 0.199 0.024
Cumulative Var 0.288 0.552 0.755 0.954 0.978

5.5.7 Orthogonal Rotation with Loadings > .70


Loadings:
         RC1    RC3    RC2   
thick            0.937       
width     0.795              
length    0.885              
volume    0.709              
density                 0.962
weight                       
surface   0.843              
crosssec  0.967              
edge      0.903              
diagonal  0.923              
cost                    0.933

                 RC1   RC3   RC2
SS loadings    5.564 2.265 2.233
Proportion Var 0.506 0.206 0.203
Cumulative Var 0.506 0.712 0.915
Desjardins, Christopher D, and Okan Bulut. 2018. Handbook of Educational Measurement and Psychometrics Using r. CRC Press.
Preacher, Kristopher J., and Robert C. MacCallum. 2003. “Repairing Tom Swifts electric Factor Analysis Machine.” Understanding Statistics 2 (1): 13–43. https://doi.org/10.1207/s15328031us0201_02.